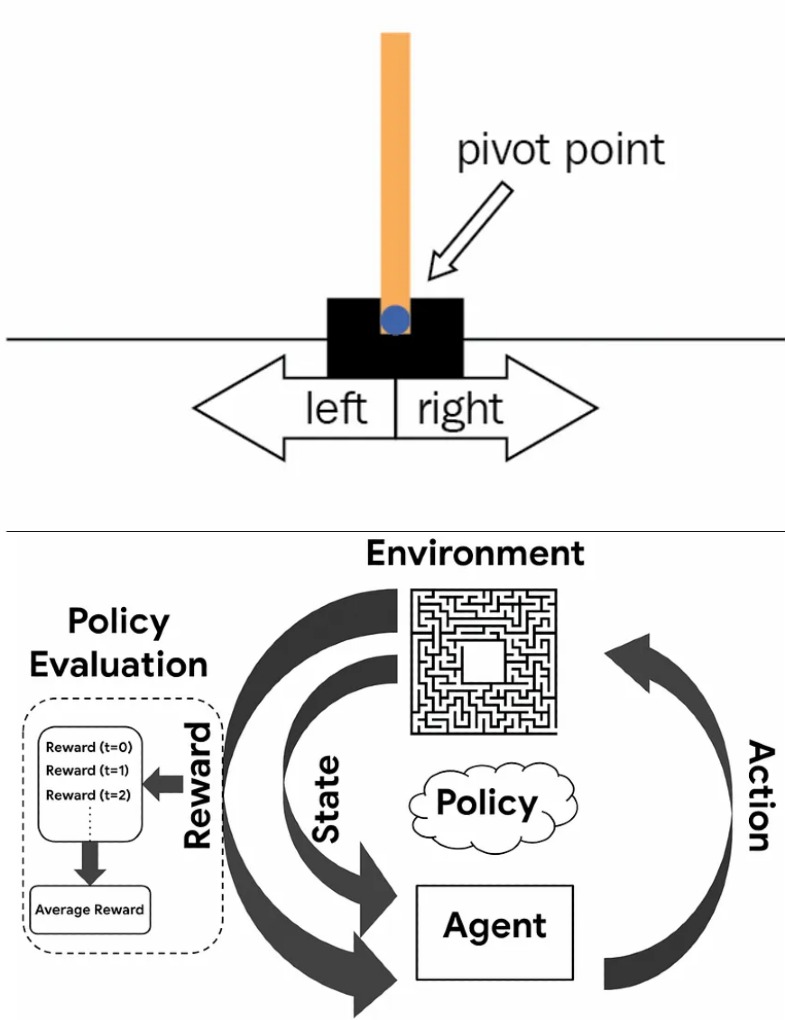
Cartpole using Q-learning

📋 Project Overview

The Cartpole Q-learning project demonstrates the application of reinforcement learning to solve a classic control problem. The cartpole (inverted pendulum) is a fundamental benchmark in control theory and reinforcement learning, where an agent must learn to balance a pole on a moving cart by applying forces left or right.

This project implements Q-learning, a value-based reinforcement learning algorithm, to train an agent that can successfully balance the pole. The implementation includes state discretization, Q-table management, exploration-exploitation strategies, and performance visualization.

💡 Problem Statement

The cartpole problem presents several learning challenges:

• Continuous State Space: Cart position, velocity, pole angle, and angular velocity are continuous
• Discrete Actions: Only two actions available: push left or push right
• Delayed Rewards: Agent receives reward only when pole stays balanced
• Exploration vs Exploitation: Balancing between trying new actions and using learned knowledge
• State Discretization: Converting continuous states to discrete Q-table indices
• Convergence: Ensuring the algorithm learns an optimal policy

⚡ Solution Approach

The project implements Q-learning with the following components:

• State Discretization: Binning continuous state variables into discrete buckets
• Q-Table: Multi-dimensional table storing Q-values for state-action pairs
• Epsilon-Greedy Policy: Exploration strategy with decaying epsilon
• Q-Learning Update: Temporal difference learning to update Q-values
• Reward Shaping: Designing reward function for effective learning
• Episode Management: Training over multiple episodes with reset conditions

🛠️ Technical Implementation

Q-Learning Algorithm

• State Space: [cart_position, cart_velocity, pole_angle, pole_angular_velocity]
• Action Space: {0: push_left, 1: push_right}
• Q-Table Initialization: Random or zero initialization
• Q-Update Rule: Q(s,a) = Q(s,a) + α[r + γ*max(Q(s',a')) - Q(s,a)]
• Learning Rate (α): Controls update magnitude
• Discount Factor (γ): Values future rewards
• Epsilon Decay: Gradually reduces exploration over time

Implementation Details

• Environment: OpenAI Gym CartPole-v1 or custom implementation
• State Discretization: Uniform or adaptive binning strategies
• Reward Function: +1 for each step pole remains balanced
• Episode Termination: When pole falls or max steps reached
• Training Loop: Multiple episodes with Q-table updates
• Evaluation: Testing learned policy without exploration
• Visualization: Plotting learning curves and episode rewards

📚 Key Learnings

• Reinforcement Learning: Understanding the fundamentals of RL and Q-learning
• Markov Decision Process: Modeling problems as MDPs with states, actions, and rewards
• Value Functions: Learning action-value functions (Q-functions)
• Exploration Strategies: Epsilon-greedy and other exploration techniques
• State Discretization: Converting continuous to discrete state spaces
• Hyperparameter Tuning: Impact of learning rate, discount factor, and epsilon

🚀 Future Enhancements

• Deep Q-Network (DQN) for handling continuous states without discretization
• Double DQN and Dueling DQN for improved stability and performance
• Prioritized Experience Replay for more efficient learning
• Multi-agent reinforcement learning for competitive scenarios
• Transfer learning to adapt to variations of the cartpole problem
• Policy gradient methods (REINFORCE, Actor-Critic) for comparison
• Real-world hardware implementation on physical cartpole system

Skills Demonstrated